Una técnica de visualización de datos que utiliza barras de superficie proporcional a la frecuencia de los valores numéricos representados y agrupados en intervalos de valores.
Descripción
Un histograma es una representación gráfica de la distribución de frecuencias de un conjunto de datos continuos o agrupados en intervalos. Es una herramienta fundamental en la estadística descriptiva para visualizar cómo se distribuyen los valores de una variable.
Componentes y funcionamiento
Un histograma se compone de la siguiente manera:
- Eje horizontal (eje x): Representa la variable de interés (por ejemplo, altura, peso, tiempo) dividida en intervalos o clases consecutivos. Estos intervalos no deben superponerse.
- Eje vertical (eje y): Representa la frecuencia (absoluta, relativa o porcentual) con la que los datos caen dentro de cada intervalo.
- Barras: El histograma utiliza barras rectangulares adyacentes (sin espacio entre ellas, a diferencia de un gráfico de barras simple) donde:
- La base de cada barra coincide con la amplitud del intervalo en el eje x.
- La altura de cada barra es proporcional a la frecuencia del intervalo. En algunos casos, especialmente cuando las amplitudes de los intervalos son desiguales, la altura representa la densidad de frecuencia (frecuencia dividida por la amplitud del intervalo), de modo que el área de la barra es lo que realmente representa la frecuencia.
El histograma permite:
- Visualizar la forma de la distribución de los datos (simétrica, asimétrica, unimodal, bimodal, etc.).
- Identificar la tendencia central (dónde se acumulan la mayoría de los datos).
- Detectar la dispersión o variabilidad de los datos.
- Localizar valores atípicos o outliers que se encuentren lejos del cuerpo principal de la distribución.
Comparación histograma/gráfico de barras
La representación gráfica de un histograma es parecida a la de un gráfico de barras, pero se diferencia en el tipo de datos estadísticos y en la organización por intervalos.
| Histograma | Gráfico de barras | |
|---|---|---|
| Tipo de datos | Se usa para datos continuos o para datos agrupados en intervalos. | Se usa para datos categóricos o discretos. |
| Representación gráfica | Las barras están pegadas para simbolizar la continuidad de la variable. | Las barras están separadas porque las categorías son distintas e independientes. |
| Función | Muestra la distribución de la variable. | Muestra la comparación entre categorías. |
Tipos de histogramas
- histograma de frecuencias absolutas
- histograma de frecuencias relativas
- función densidad
- curva acumulativa u ojiva
- curva acumulativa de frecuencias absolutas
Ejemplos
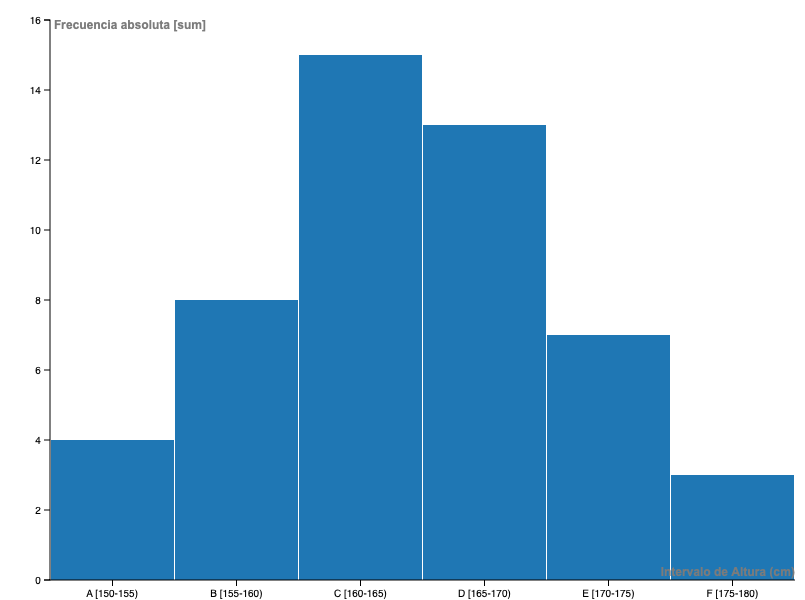
Distribución de frecuencias de la altura de 50 estudiantes
Vamos a visualizar la distribución de altura de los 50 estudiantes de un curso. Las dimensiones, en este caso, son valores continuos, puesto que corresponden a intervalos de 5 centímetros cada uno.
La distribución absoluta es la siguiente:
- A [150-155): 4 estudiantes.
- B [155-160): 8 estudiantes.
- C [160-165): 15 estudiantes.
- D [165-170): 13 estudiantes.
- E [170-175): 7 estudiantes.
- F [175-180): 3 estudiantes.
- Total: 50 estudiantes.
| Intervalo de altura (cm) | Frecuencia absoluta |
|---|---|
| A [150-155) | 4 |
| B [155-160) | 8 |
| C [160-165) | 15 |
| D [165-170) | 13 |
| E [170-175) | 7 |
| F [175-180) | 3 |
Esta tabla es ideal para construir un histograma por los siguientes motivos:
- Variable continua: La altura es una variable continua, lo que quiere decir que puede tomar cualquier valor dentro de un rango (ej. 162.3 cm, 162.45 cm).
- Intervalos (clases): El eje horizontal del histograma se define por estos intervalos (ej., de 150 a 155 cm).
- La notación [150−155) significa que incluye 150 cm pero excluye 155 cm.
- Los intervalos son consecutivos y no se superponen, lo que permite que las barras del histograma estén juntas.
- Frecuencia absoluta (f i): Este es el valor que define la altura de cada barra del histograma. Indica cuántos estudiantes caen dentro de cada rango de altura.
- Histograma: Al dibujar el histograma, los intervalos de altura irán en el eje x y la frecuencia absoluta (f i), en el eje y.